Finally, a fun(ish) promo that doesn’t require flights or nights…
On Monday, Deals We Like published a cool idea in the post “Spend $46 and Earn at Least 47,000 IHG Points!” IHG (Intercontinental Hotels Group) has an upcoming promotion called Priceless Surprises. Unlike most airline and hotel promotions, this one does not require travel. The promo offers two ways to earn “Priceless Surprises”: 1) Complete two eligible stays; or 2) Mail in a hand-printed 3” X 5” piece of paper.
Full rules for both options can be found in the IHG and MasterCard®Priceless Surprises® Promotion Official Rules document.
In this post, we’ll look only at the mail-in option…
Number of entries
The official rules state “Each entrant is eligible to receive up to ninety-four (94) Game plays during the Promotion Period, regardless of method of entry.” So, the idea here is to mail in up to 94 separate entries and rack in the points. How many points will you get from doing so? Let’s see…
Chance of winning analysis
Prizes are grouped into Group A, Group B, and Group C. The Group A prizes are where you’ll find the really good stuff. Prizes range from $50 prepaid cards to all-expense paid trips to Paris or New York. The Group A prizes do not have fixed odds of winning. Instead, they’ve decided how many of each prize will be awarded (3 Paris trips, 2 one million IHG point winners, 525 free night winners, 1050 $50 gift card winners, etc.). So, your chance of winning will depend upon how many competing entries show up.
Group B and C prizes are IHG points. The odds of winning each of these is as follows:
| Prize | Odds |
| 5000 points | 1:42.86 |
| 2000 points | 1:28.57 |
| 1000 points | 1:14.29 |
| 500 points | 1:1.18 |
I (and many others) initially read the odds incorrectly as probabilities. For example, the 500 point prize odds of winning is listed as 1:1.18. If you think of this as a probability (1 out of 1.18 entries will win), then it looks like you have a 85% chance of winning this prize. And, if you add up all of the options, it looks like you have nearly 100% chance of winning something. In truth, though, 1:1.18 should be read as “for every 1 win, there will be 1.18 losses”. In other words, the probability of winning 500 points is 1 / (1+1.18) = 46%.
My first draft of this post was based upon the incorrect conversion of odds to probabilities described above. Luckily, before publishing, I read this comment by JEM in the Deals We Like post:
Hmm… If I remember my middle school math correctly, Odds and Probability have this relationship:
Odds = (# of Favorable Outcomes) : (# of Unfavorable Outcomes)
Probability = F / (F + U)So the probability of winning on any single turn is:
P(5000) = 1 / (1 + 42.86) = 0.0228 = 2.28%
P(2000) = 1 / (1 + 28.57) = 0.0338 = 3.38%
P(1000) = 1 / (1 + 14.29) = 0.0654 = 6.54%
P(500) = 1 / (1 + 1.18) = 0.4587 = 45.87%In other words, you can expect to win SOMETHING only about 58% of the time.
The expected point value for each turn would then be SUM(P(q) * q) for each possible outcome q.
EV(5000) = 0.0228 * 5000 = 114
EV(2000) = 0.0338 * 2000 = 67.6
EV(1000) = 0.0654 * 1000 = 65.4
EV(500) = 0.4587 * 500 = 229.4
EV(0) = 0.4193 * 0 = 0
EV(Turn) = 476.4 points per turnwhich would SEEM to indicate a total Expected Value of 44,782 points over the maximum 94 turns.
HOWEVER, that overstates what’s possible. You can only win a maximum of 5 total prizes > 500, so even if you maxed out by hitting five 5K prizes (astronomically unlikely), your MAXIMUM possible value would be
MAX(5x5K) = (5 * 5000) + (500 * 89) = 69,500 points
with an approximate expected value of
EV(5x5K) = (5 * 5000) + (0.4587 * 500 * 89) = 45,412
which is just barely above the naive EV.
And if you were “unlucky” enough to hit five 1K prizes, your maximum possible value would be
MAX(5 * 1K) = (5 * 1000) + (500 * 89) = 49,500 points
with an expected value of approximately 25,412 points, or 270 points per turn.
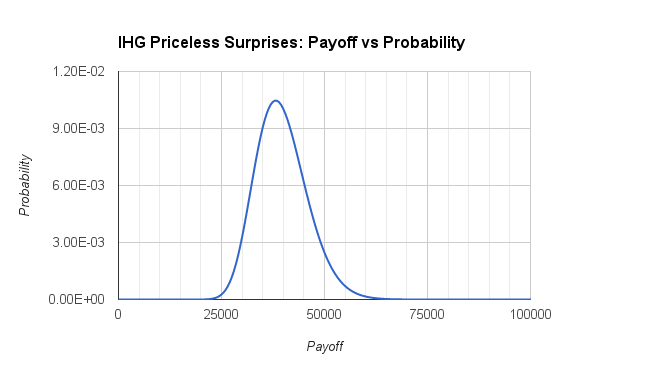
FWIW, I modeled 94 turns with the probabilities above and the cap of 5 high-value prizes. Over a couple of million iterations, I got these results:
MIN: 17,500
MAX: 54,000
AVG: 31,657
STD DEV: 4,158If I’m correct, that would predict that 95% of people who play 94 times will receive between 23,000 and 40,000 points, with less than 0.2% exceeding 44,000.
Good stuff from JEM! To summarize:
- For those who do not win the group A prizes, the chance of winning something is about 58%
- If you “play” 94 times, you are very likely to win a total of between 23,000 and 40,000 points.
Later, ‘Dem Flyers followed up with a similar analysis (see: Before you go off writing 94 postcards…). In this post, they came up with slightly different numbers, but the same overall theme:
- Across all entries which do not win the group A prizes, the average (mean) result will be 476.4 IHG points.
- If you “play” 94 times, you are very likely to win between 30,000 and 50,000 points.
Why did ‘Dem Flyers come up with a higher range than JEM? JEM answered in this comment:
I can’t tell for sure since I can barely read Java code, but from your data set, it appears that you’re significantly overestimating the expected value. The Ts&Cs state that you can only win a total of 5 (any combination) of the “Group B” prizes (1000, 2000, or 5000 points). After you win 5, you’ll only have the 46% chance of winning 500 points. Thus the maximum possible return is 5*5000 + 89*500 = 69,500. Your data set shows small, but non-zero probabilities all the way up to 445,000.
I modeled the contest using that constraint, and my expected value for 94 entries dropped to about 31,600 (336 points per entry, well below your stated 476) with a StdDev of 4100, so 95% of the total returns should fall within the range 23K-40K points and less than 0.2% of results should go higher than 44K.
Aha! I had missed that, but sure enough, as JEM wrote, there is a 5 prize per person limit to Group B prizes:
Limit: One (1) prize from Group A and five (5) prizes from Group B prize per person.
Chance of winning summary
I’ll leave it to others to check JEM’s math. It looks reasonable to me. So:
- The chance of winning something with each entry is about 58%
- If you “play” 94 times, you are very likely to win a total of between 23,000 and 40,000 points.
Is it worth it?
To enter the contest without any IHG stays, you must hand write your entry on a 3 X 5 piece of paper and mail it in. If each entry takes 2 minutes of your time and 49 cents for a stamp, then your total cost for 94 entries will be:
- 188 minutes (let’s call it 3.5 hours, if we include breaks)
- $46.06
In exchange for that time and expense, you’ll likely get between 23,000 and 40,000 points. With the current Fair Trading Price of IHG points at .56 cents each, that means that you’ll likely get between $128 and $224 “worth” of points.
I’m not sure it’s worth the effort, but I’ll probably do it anyway. I haven’t yet decided, though, whether I’ll submit 94 entries for my wife as well… or my son… or my dog…


![[Reminder: Marriott GCs on 4/23] Daily Getaways 2024: Complete preview of all the deals Daily Getaways 2023](https://frequentmiler.com/wp-content/uploads/2023/06/Daily-Getaways-2023-218x150.jpg)


[…] Send us a self-addressed stamped envelope to (no don’t do this, seriously, don’t do this) […]
Can we mail them all on the same day or is it a one-per-day limit?
Just for ~ 230 $……what a work……..just automate bing rewards and u can earn more than that……..
Would 3×5 index card (inside regular envelope) work?
why not send in a 3 x 5 post card….won’t that work?
It may be educational to look over the T&Cs before deciding to send 94 post cards.
In addition to @Miles excellent recommendation, the USPS won’t deliver anything under 3.5″ x 5″, so 3 x 5 cards probably won’t be delivered…
[…] Between 23,000 and 40,000 points for $46 and a cramped hand – IHG has a new promotion and no purchase is necessary. Does it make sense to write out 94 postcards by hand to enter? […]
I wonder if they will make a cumbersome process (or actually make us “play the game”) in some time-consuming way with each email. I was just thinking of Air France’s contests where each time that you enter you have to look at different pictures and figure out what is different between similar photos. I couldn’t do this 94 times!
Dont forget the cost of 94 envelopes, which costs about 12$ after tax at staples; and 94 3×5 cards, which is about another 3 bux. so total cost is like 60$
Both of those can be bought at the dollar store – just depends how much you value the chance to use ink plus!
Hold on. It says you need to add the first 6 digits of your Mastercard with every 3 X 5 card you mail in. Can it be any MC, or does it have to be the IHG Mastercard?
Since your results are quick (I think the emails should come quickly anyway) I think it might be worth sending in 1/2 the entries right away and then see how many of the limit 5 group you have won. If it is 4 or 5 then the second half of your entries will have significantly lower returns so it might be better to start sending in for another account.
Also there is a way to automate ‘hand writing’ with a machine many women (and some men) already own. It is for paper crafts and called a Silhouette and you might want to ask if someone you know has one. HT: @kathylittle2
You should have seen my spouses face when I said we had a new activity. haha
can you do it for multiple “people”? .. i think the terms just said has to be different emails.. can it be the same IHG club #?
Your first mistake was participating in any IHG promotion. They are masters at confusion and rule changing.
I find it hard to believe that IHG would run a promotion in which, after a night’s stay, you get an email saying you’ve won an instant prize, you click the email, and 42% of the time you get NOTHING. What kind of promo is that? Something smells fishy here.
Take a look at the actual Priceless Surprise promotion site (http://pricelesssurprises.ihg.com/).
It states
“Every time you stay…you could unlock bonus points…
“Unlock your chances for a Priceless Surprise” and
“Stay. Receive 1000 bonus points for your first qualifying stay when your register and use your MasterCard. Stay Again. Receive a chance at a Priceless Surprise every time you stay and use your MasterCard”
So you get at least 1000 points (if you stay). But it sounds to me unlikely that getting a prize is a sure thing.
FYI the full Rules link now responds “The resource you are looking for has been removed, had its name changed, or is temporarily unavailable.”
You guys are killing their site. lol
Here’s the correct link now..
https://d2ukkex5d6aodv.cloudfront.net/pdf/PricelessSurprisesRules_FINAL.pdf?v=HeHVmBrb
Either we are killing their site, or IHG is changing the rules….
It’s still available from the IHG website. Hit it from there, or just take the “?v=….” off FM’s link.
I fixed the post with an updated link